本文共 2938 字,大约阅读时间需要 9 分钟。
文章目录
(1)什么是信号量
前面的叙述中,我们通过锁保证了每次只有一个线程进入临界区,但是临界区资源很多也很大,每次只允许一个线程进入往往会使效率很低。所以如果将临界区划分为多个独立的区域,划分为多少个区域就让多少个线程进入,,但是这样就同时带来了一个问题——如果划分为了5个区域,但是同时进入了10个线程该怎么办?所以这一点可以通过信号量解决。信号量可以理解为一个计数器,它用来描述临界资源的有效个数
信号量由一个值和一个指针组成,指针指向等待该信号量的线程。信号量的值表示相应资源的使用情况,比如如果S>=0表示资源够用,如果执行P操作表示请求分配一个资源,那么S就会减一;当S<0时表示已经没有可用资源(此时S的绝对值表示等待该资源的线程数)请求者必须等待其他线程释放资源方可继续运行。如果执行一个V操作就表示会释放一个资源,所以S加一
(2)与信号量相关的操作
1:要使用信号量就需要创建一个sem_t类型变量
#include//头文件sem_t sem1;
2:在使用信号量前,需要对这个变量进行初始化,使用的函数是sem_init
int sem_init(sem_t* sem,int pshared,unsigned int value);//pshared一般给0,非零表示进程间共享//value:信号量初始值
3:信号量使用完毕需要用sem_destory进行销毁
int sem_destory(sem_t* sem);
4:POSIX信号量中的P操作对应的接口是sem_waitm,V操作对应的接口是sem_post
int sem_wait(sem_t* sem);int sem_post(sem_t* sem);
(3)基于环形队列的生产者与消费者模型-信号量(单消费者单生产者)
基于阻塞队列的生产者与消费者模型存在一个很大的问题就是他们其实是在串行运行的,并没有并行运行,这就导致他们的效率不是很高,而使用环形队列则可以解决这个问题。
在这里,我们使用的载体是环形队列,他和数据结构的循环队列基本一致,在这里就不做过多介绍了,具体请移步如下在这样的模型中,消费者和生产者都有各自的P,V操作,消费者关心的是队列中有没有数据,所以它进行P操作时申请的是数据,而进行V操作时归还的是空格资源;生产者关系的是队列中有没有空格,所以它进行P操作时申请的是空格,而进行V操作时由于生产好了数据归还的就是数据
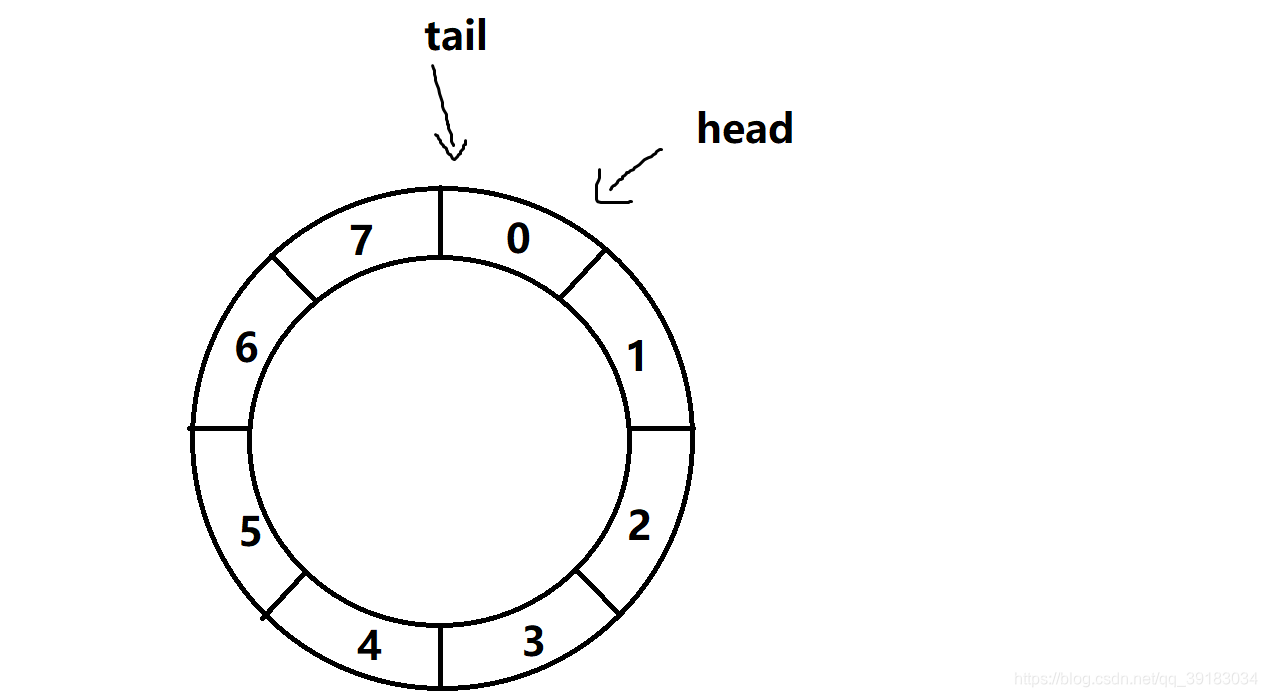
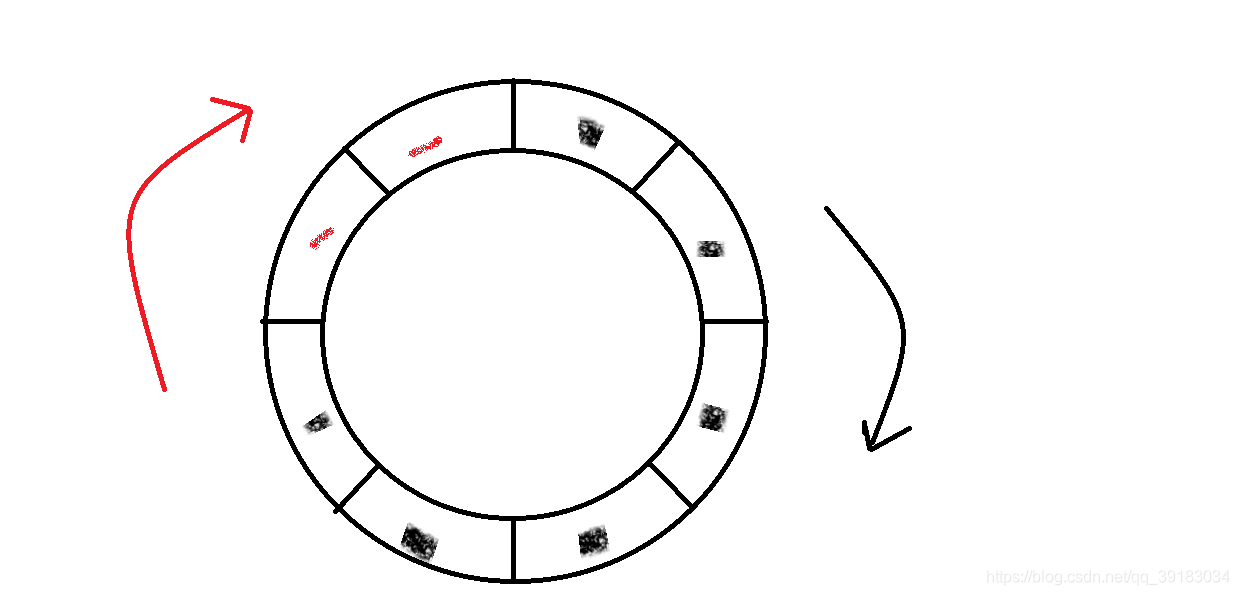 如下,我们使用POSIX信号量。利用唤醒队列重写这个消费者生产者模型。
如下,我们使用POSIX信号量。利用唤醒队列重写这个消费者生产者模型。 circular_queue.hpp如下 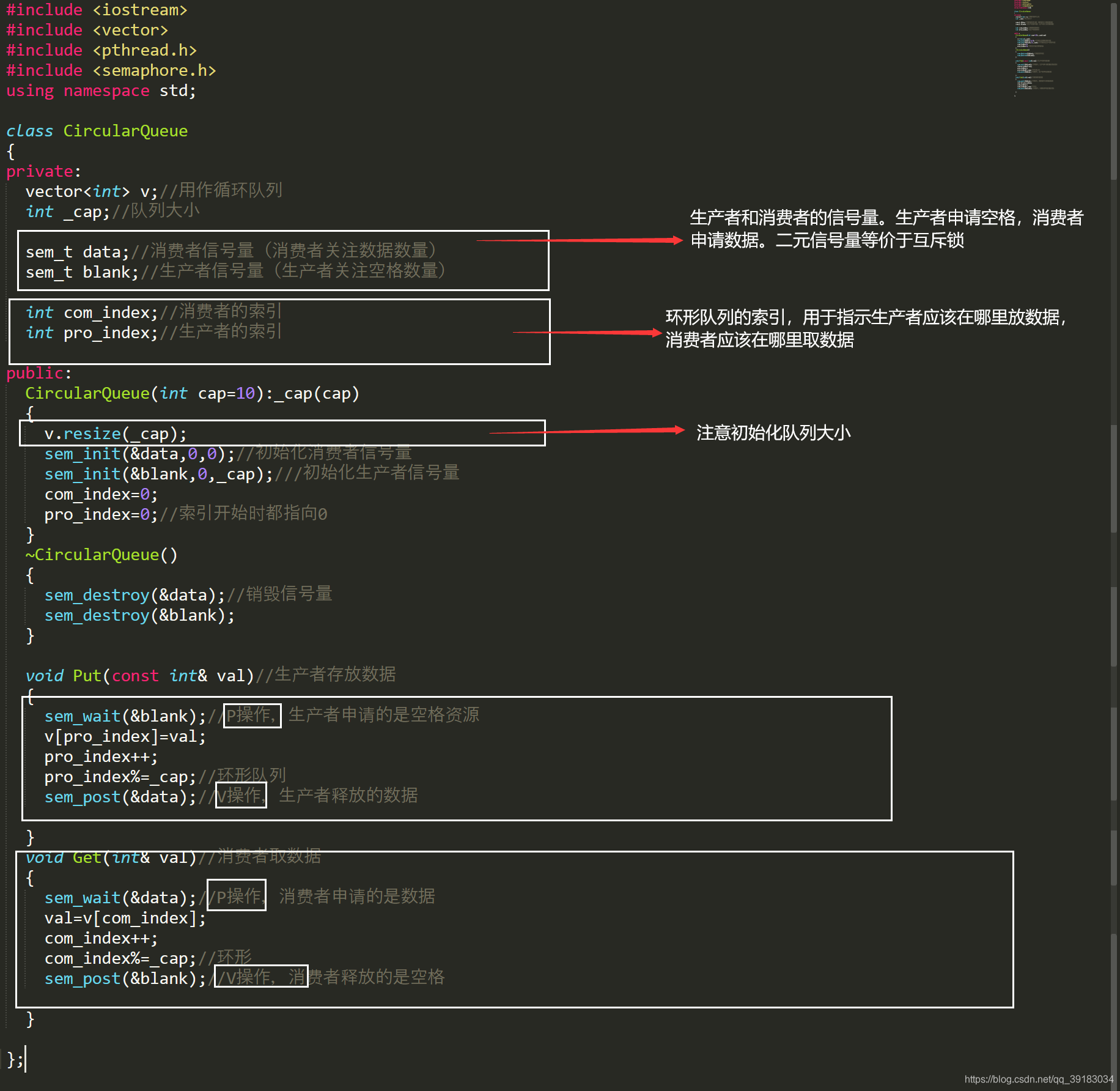
#include#include #include #include using namespace std;class CircularQueue{ private: vector v;//用作循环队列 int _cap;//队列大小 sem_t data;//消费者信号量(消费者关注数据数量) sem_t blank;//生产者信号量(生产者关注空格数量) int com_index;//消费者的索引 int pro_index;//生产者的索引public: CircularQueue(int cap=10):_cap(cap) { v.resize(_cap); sem_init(&data,0,0);//初始化消费者信号量 sem_init(&blank,0,_cap);///初始化生产者信号量 com_index=0; pro_index=0;//索引开始时都指向0 } ~CircularQueue() { sem_destroy(&data);//销毁信号量 sem_destroy(&blank); } void Put(const int& val)//生产者存放数据 { sem_wait(&blank);//P操作,生产者申请的是空格资源 v[pro_index]=val; pro_index++; pro_index%=_cap;//环形队列 sem_post(&data);//V操作,生产者释放的数据 } void Get(int& val)//消费者取数据 { sem_wait(&data);//P操作,消费者申请的是数据 val=v[com_index]; com_index++; com_index%=_cap;//环形 sem_post(&blank);//V操作,消费者释放的是空格 }};
test.cpp如下
#include "circular_queue.hpp"#includeCircularQueue* bq=new CircularQueue(10);void* consumer_run(void* arg){ while(1) { int data; bq->Get(data); printf("%s拿到数据:%d\n",(char*)arg,data); }}void* productor_run(void* arg){ int cout=1; while(1) { if(cout==11) cout=1; bq->Put(cout); printf("%s放进数据:%d\n",(char*)arg,cout); cout++; sleep(1); }}int main(){ pthread_t con,pro; pthread_create(&con,nullptr,consumer_run,(void*)"消费者"); pthread_create(&pro,nullptr,productor_run,(void*)"生产者"); pthread_join(con,nullptr); pthread_join(pro,nullptr); delete bq; return 0;}
效果如下,在这里限制生产者的速度,所以每当生产者生产一个的时候消费者才能消费。更多的时候,消费者生产者是并行的
(生产者慢,消费者快)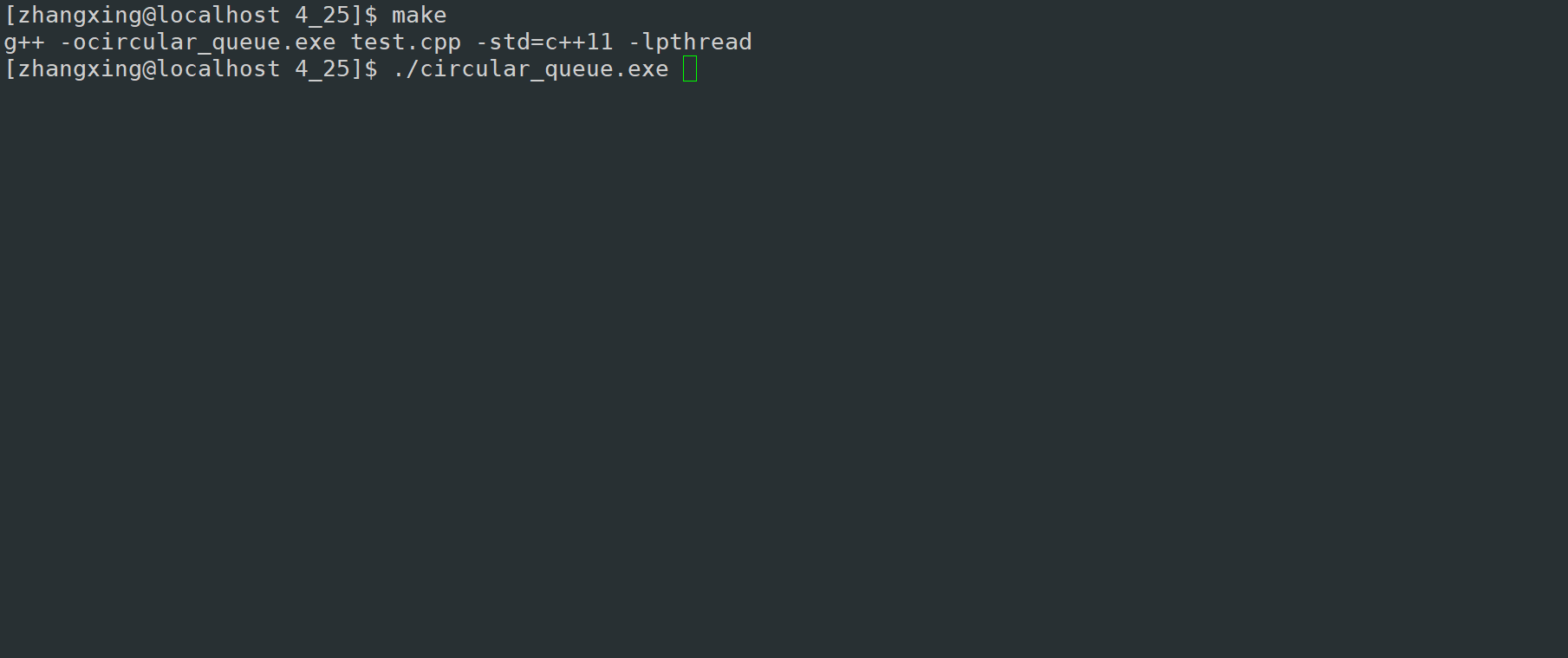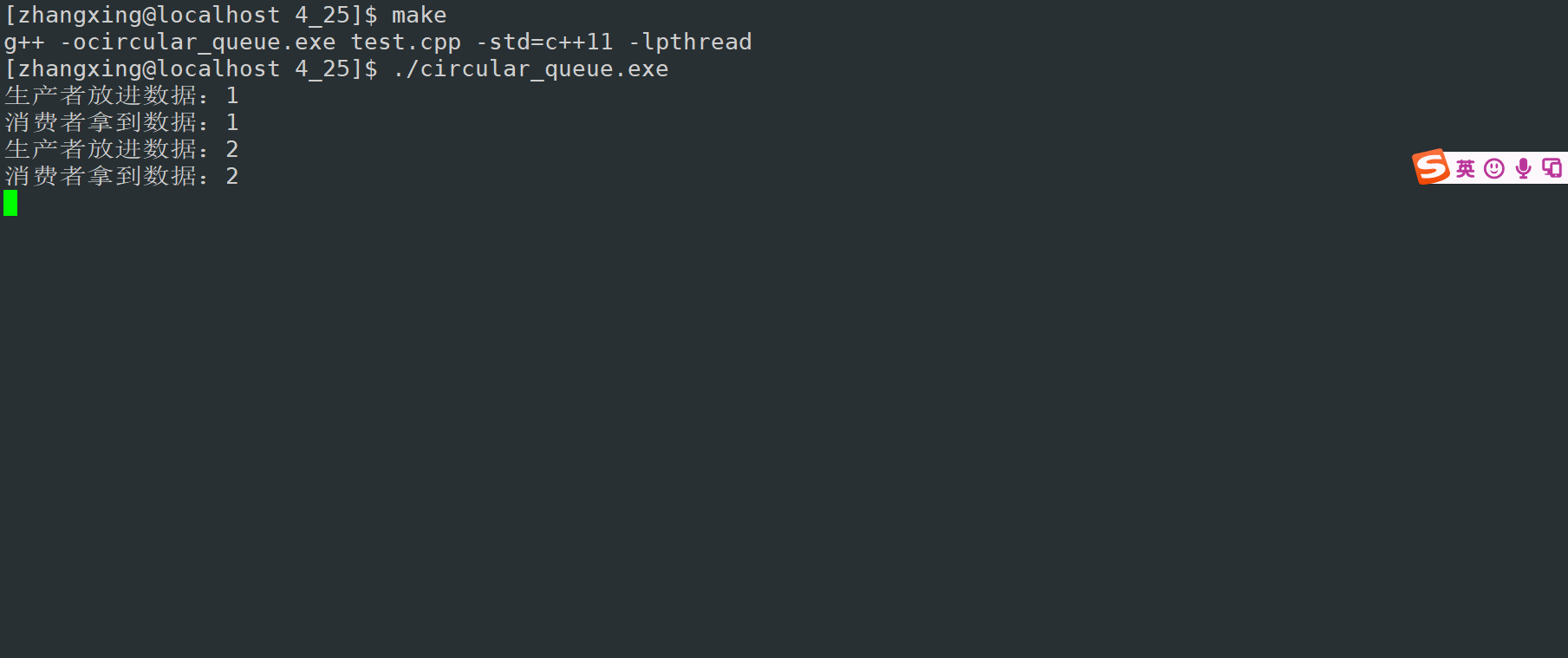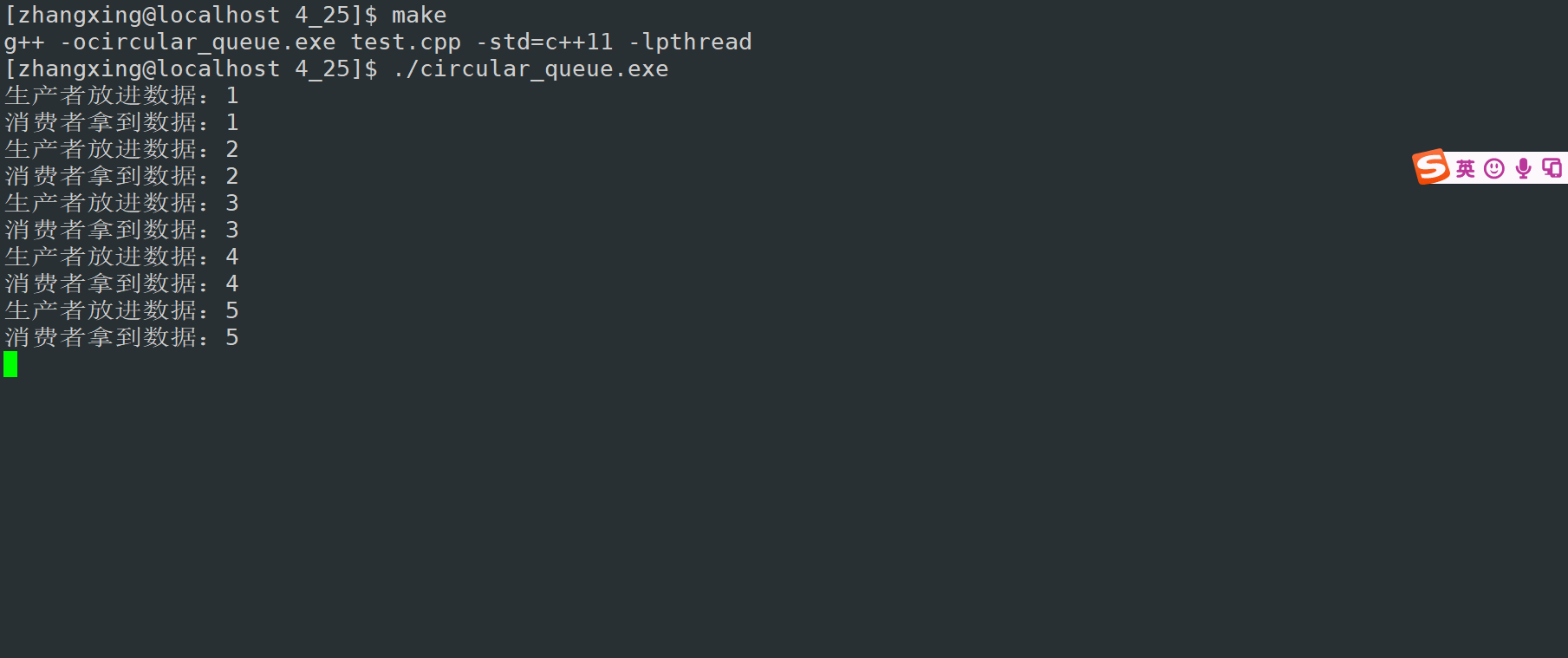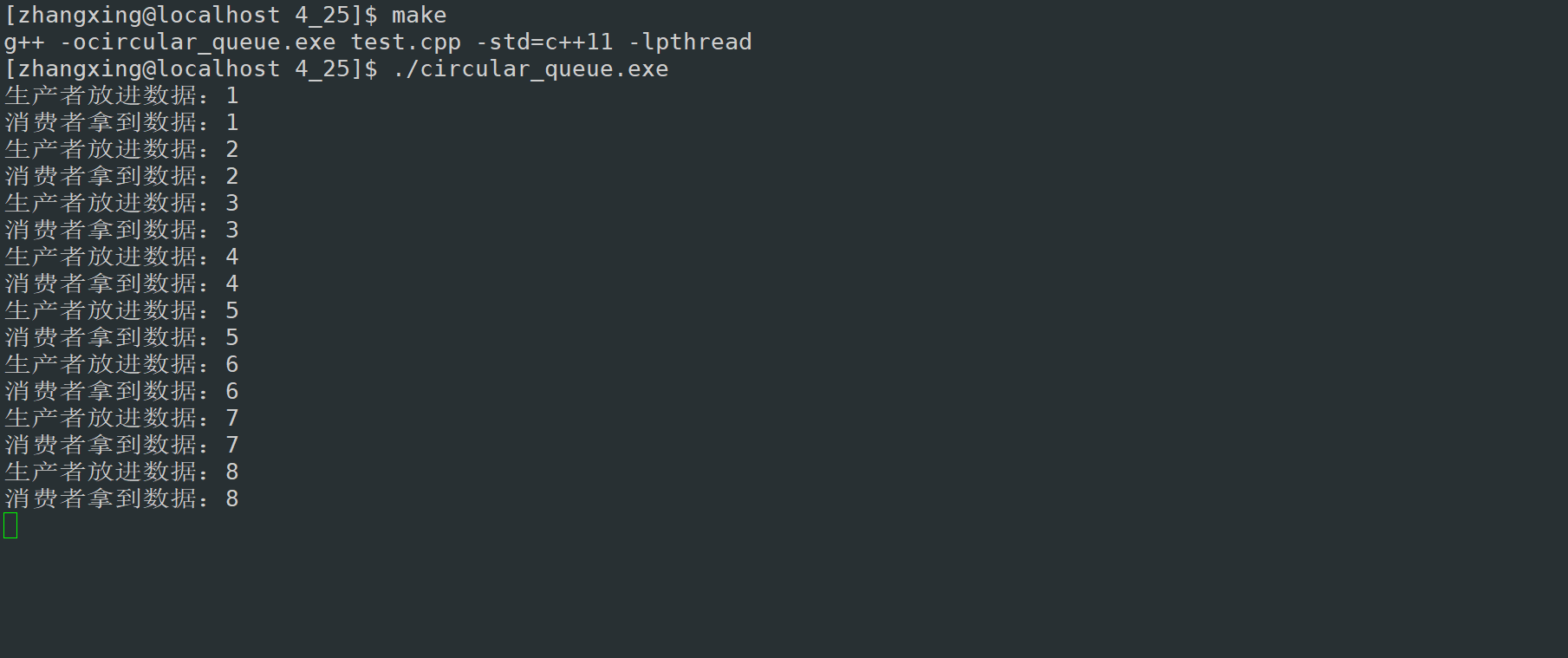
转载地址:http://visi.baihongyu.com/